Cálculo de áreas entre dos graficas

De esta clase no me quedo muy claro cómo resolverlos solo que con la nota que nos dio me estoy ayudando un poco ya que se me dificulto realizar el ejercicio en clases 

Podemos encontrar el área entre dos curvas al encontrar el área bajo cada curva separadamente. Luego, podemos restar estas áreas de modo que obtengamos el área de intersección. Podemos aplicar este principio no solamente con curvas, sino también con los ejes del plano.

EJERCICIO 1

Si es que tenemos las curvas �=�2+1 y �=−�2+3, ¿cuál es el área de la región de intersección?

Solución

Podemos empezar encontrando los puntos de intersección de las curvas para determinar los límites de la región. Entonces, tenemos:

�2+1=−�2+3

2�2=2

�=±1

Podemos trazar una gráfica para visualizar el área requerida:

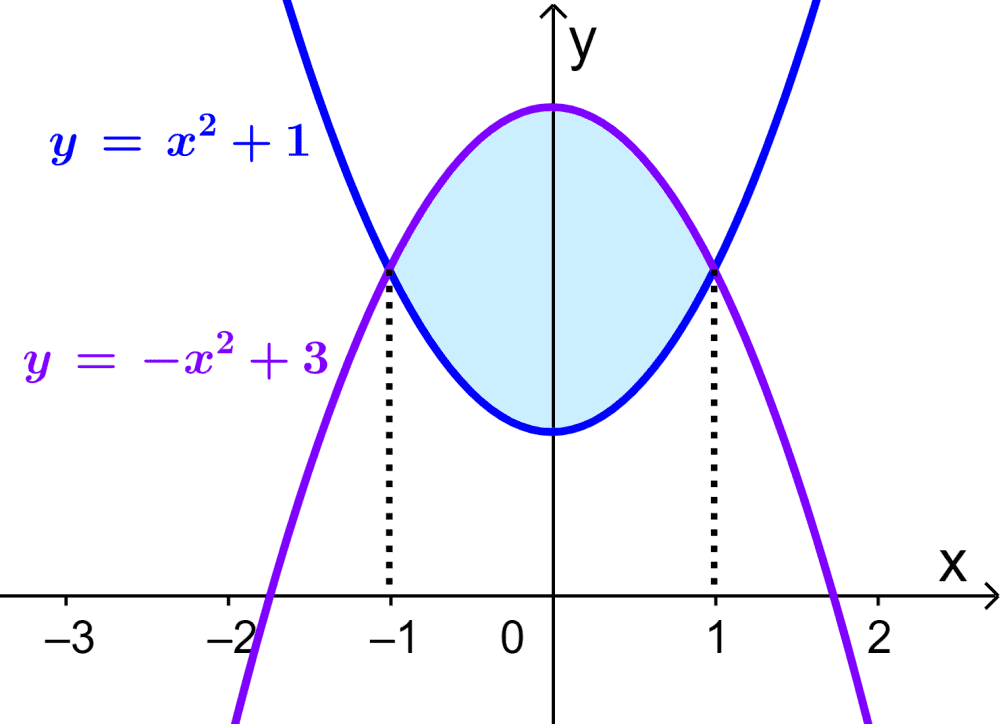
ejemplo 1 area entre dos curvas

El área de la región puede ser obtenida restando el área bajo la curva �=�2+1 del área bajo la curva �=−�2+3. Entonces, tenemos:

�=∫−11(−�2+3)��−∫−11(�2+1)��

=∫−11(−�2+3)–(�2+1)��

=∫−11(−2�2+2)��

=[−2�33+2�]−11

=[−23+2]−[23−2]

=43+43

=83

El área de la región de intersección de las dos curvas es 83.

EJERCICIO 2

¿Cuál es el área formada por la intersección de �=−13�2+3 y la recta �=�+3?

Solución

Similar al ejercicio anterior, tenemos que empezar encontrando los puntos de intersección de la recta y la curva. Entonces, tenemos:

�+3=−13�2+3

13�2+�=0

�(13�+1)=0

�=−3   o   �=0

Ahora, podemos trazar una gráfica para visualizar el área requerida:

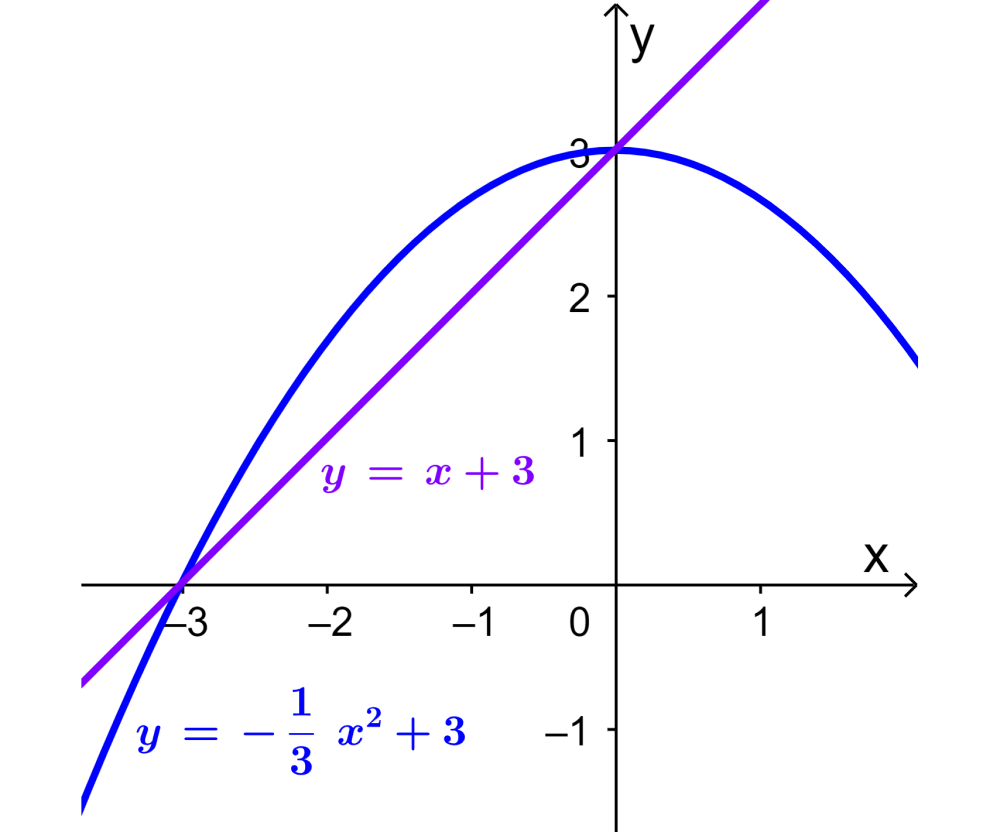
Ejemplo2 de area entre dos curvas

Entonces, vemos que el área de la región está dada por el área de la recta menos el área de la curva. Es decir, tenemos:

�=∫−30(−13�2+3)��−∫−30(�+3)��

=∫−30(−13�2+3)–(�+3)��

=∫−30(−13�2−�)��

=[−�39−�22]−30

=[−039−022]−[−(−3)39−(−3)22]

=−[3−92]

=32

El área de la región de intersección de las dos curvas dadas es 1.5.



Área entre dos curvas - Ejercicios resueltos - Neurochispas

Comentarios

Publicar un comentario

Entradas más populares de este blog

Imagen
  Integración de potencias de funciones trigonométricas  En esta clase comprendí a la manera de cómo puedes realizar este modo de integración y como se tiene que utilizar el cambio de variable para su finalización  integrar expresiones que contienen términos elevados a potencias enteras o fraccionarias de funciones trigonométricas. Aquí tienes algunas fórmulas generales que pueden ser útiles: Integración de seno y coseno elevados a potencias pares: ∫ sin ⁡ � ( � )   � � = − 1 � ⋅ sin ⁡ � − 1 ( � ) ⋅ cos ⁡ ( � ) + � − 1 � ∫ sin ⁡ � − 2 ( � )   � � ∫ sin n ( x ) d x = − n 1 ​ ⋅ sin n − 1 ( x ) ⋅ cos ( x ) + n n − 1 ​ ∫ sin n − 2 ( x ) d x ∫ cos ⁡ � ( � )   � � = 1 � ⋅ cos ⁡ � − 1 ( � ) ⋅ sin ⁡ ( � ) + � − 1 � ∫ cos ⁡ � − 2 ( � )   � � ∫ cos n ( x ) d x = n 1 ​ ⋅ cos n − 1 ( x ) ⋅ sin ( x ) + n n − 1 ​ ∫ cos n − 2 ( x ) d x Integración de tangente elevada a una potencia impar: ∫ tan ⁡ � ( � )   � � = 1 � − 1 ⋅ tan ⁡ � − 1 ( � ) − ∫ tan ⁡ � − 2 ( � )   � � ∫ tan n ( x ) d x ...
Leer más
Imagen
Integrales indefinidas   En esta clase de cálculo integral nos dieron las fórmulas para resolver problemas con respecto a este curso que llevaremos en lo personal con los problemas que nos presentó en clases mire que no se ven tan complicadas, pero solo es el comienzo.            :") Una integral indefinida, también conocida como antiderivada, es una operación en cálculo que se utiliza para encontrar una función cuya derivada sea igual a una función dada. Se representa de la siguiente manera: ∫ f(x) dx En esta notación, ∫ representa el símbolo de integral, f(x) es la función que deseas integrar y dx indica que estás integrando con respecto a la variable x. El resultado de esta operación es una función, generalmente acompañada de una constante arbitraria de integración (denotada como "C"). La integral indefinida se utiliza para encontrar una familia de funciones que tienen la misma derivada que la función dada. Por lo tanto, una integral indefinida...
Leer más
Imagen
 VALOR ESPERADO Y VARIANZA DE UNA VARIABLE ALEATORIA DISCRETA Media o valor esperado La media «µ» o valor esperado «E(X)» es un promedio ponderado de los valores que asume la variable aleatoria cuando los pesos son las probabilidades. Es una medida de tendencia central. Cuando trabajamos con una variable aleatoria discreta, la media o valor esperado se calcula mediante la siguiente fórmula: Como verás, la media  µ  de una variable aleatoria discreta X se encuentra al multiplicar cada posible valor de X por su propia probabilidad y luego sumar todos los productos. El valor esperado o media no tiene que ser un valor que la variable aleatoria pueda asumir.   Varianza L varianza,  σ 2  o  V(X),  es un promedio ponderado de las desviaciones al cuadrado de una variable aleatoria de su media. Los pesos son las probabilidades. La varianza  σ 2  o  V(X)  se calcula con la siguiente fórmula: Pero es más fácil y rápido usar esta fórm...
Leer más