REGLAS DE DERIVACION ALGEBRAICAS


En esta clase aprendí las diferentes reglas en las que podemos llegar a resolver una derivada de y´ de mare más fácil a un que la verdad durante la clase entendí como realizarlas y al estar viendo videos me llego una manera más clara de resolverlos 

La notación más usual para representar la derivada de una función y=f(x) es la que acabamos de ver (f’ o y’). Sin embargo, otra notación muy usada es la notación de Leibniz que se representa como cualquiera de las siguientes expresiones:

En vista de que la derivada es en esencia un límite, esta puede existir o no, pues los límites no siempre existen. En caso de que exista, se dice que la función en cuestión es diferenciable en el punto dado.

Función algebraica

Una función algebraica es una combinación de polinomios por medio de sumas, restas, productos, cocientes, potencias y radicales.

Un polinomio es una expresión de la forma

Pn=anxn+ an-1xn-1+ an-2xn-2+…+ a2x2+ a1x+a0

Donde n es un número natural y todos los ai, con i=0,1,…,n, son números racionales y an≠0. En este caso se dice que el grado de este polinomio es n.

Los siguientes son ejemplos de funciones algebraicas:

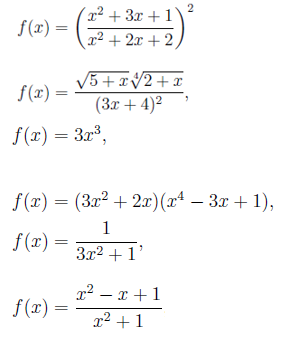
Aquí no están incluidas las funciones exponenciales, logarítmicas y trigonométricas. Las reglas de derivación que veremos a continuación son válidas para funciones en general, pero nos restringiremos y las aplicaremos en el caso de funciones algebraicas.

Reglas de derivación

Derivada de una constante

Establece que la derivada de una constante es cero. Es decir, si f(x)=c, entonces f’(x)=0. Por ejemplo, la derivada de la función constante 2 es igual a 0.

Derivada de una potencia

Si f(x)=xn, entonces f’(x)=nxn-1. Por ejemplo, la derivada de x3 es 3x2. Como consecuencia de esto, se obtiene que la derivada de la función identidad f(x)=x es f’(x)=1x1-1=x0=1.

Otro ejemplo es el siguiente: sea f(x)=1/x2, entonces f(x)=x-2 y f’(x)=-2x-2-1=-2x-3.

Esta propiedad también es válida raíces, pues las raíces son potencias racionales y se puede aplicar lo anterior también en ese caso. Por ejemplo, la derivada de una raíz cuadrada viene dada por 


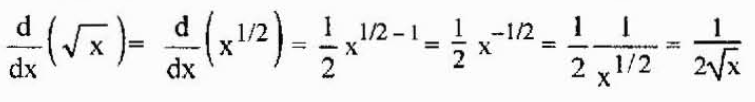
Derivada de una suma y de una resta

Si f y g son funciones diferenciables en x, entonces la suma f+g también lo es y se cumple que (f+g)’(x)=f’(x)+g’(x).

Análogamente se tiene que (f-g)’(x)=f’(x)-g’(x). En otras palabras, la derivada de una suma (resta), es la suma (o resta) de las derivadas.

Ejemplo

Si h(x)=x2+x-1, entonces

h’(x)=(x2)+(x)’-(1)’=2x+1-0=2x+1.

Derivada de un producto

Si f y g son funciones diferenciables en x, entonces el producto fg también es diferenciable en x y se cumple que

(fg)’(x)=f’(x)g(x)+f(x)g’(x).

Como consecuencia se tiene que si c es una constante y f es una función diferenciable en x, entonces cf también es diferenciable en x y (cf)’(x)=cf’(X).

Ejemplo

Si f(x)=3x(x2+1), entonces

f’(x)=(3x)’(x2+1)+(3x)(x2+1)’=3(x)’(x2+1)+3x[(x2)’+(1)’]

=3(1)( x2+1)+3x[(2x2-1)+0]=3(x2+1)+3x(2x)=3x2+3+6x2

=9x2+3.
















reglas_de_derivacion.png (598×415) (fisimat.com.mx)



Comentarios

Publicar un comentario

Entradas más populares de este blog

Imagen
  Integración de potencias de funciones trigonométricas  En esta clase comprendí a la manera de cómo puedes realizar este modo de integración y como se tiene que utilizar el cambio de variable para su finalización  integrar expresiones que contienen términos elevados a potencias enteras o fraccionarias de funciones trigonométricas. Aquí tienes algunas fórmulas generales que pueden ser útiles: Integración de seno y coseno elevados a potencias pares: ∫ sin ⁡ � ( � )   � � = − 1 � ⋅ sin ⁡ � − 1 ( � ) ⋅ cos ⁡ ( � ) + � − 1 � ∫ sin ⁡ � − 2 ( � )   � � ∫ sin n ( x ) d x = − n 1 ​ ⋅ sin n − 1 ( x ) ⋅ cos ( x ) + n n − 1 ​ ∫ sin n − 2 ( x ) d x ∫ cos ⁡ � ( � )   � � = 1 � ⋅ cos ⁡ � − 1 ( � ) ⋅ sin ⁡ ( � ) + � − 1 � ∫ cos ⁡ � − 2 ( � )   � � ∫ cos n ( x ) d x = n 1 ​ ⋅ cos n − 1 ( x ) ⋅ sin ( x ) + n n − 1 ​ ∫ cos n − 2 ( x ) d x Integración de tangente elevada a una potencia impar: ∫ tan ⁡ � ( � )   � � = 1 � − 1 ⋅ tan ⁡ � − 1 ( � ) − ∫ tan ⁡ � − 2 ( � )   � � ∫ tan n ( x ) d x ...
Leer más
Imagen
Integración  por partes   en esta clase aprende la nueva regla de integración y como implementarla en la practica. ¿Qué es la Integración por Partes y por qué es Importante? La integración por partes es una herramienta esencial en el campo del cálculo integral. Se basa en una versión modificada de la regla del producto en la derivación y es especialmente útil cuando necesitas encontrar la integral de un producto de dos funciones. Esta técnica es relevante en una amplia gama de aplicaciones matemáticas, científicas e ingenieriles, y es fundamental para resolver problemas en física, estadística, ingeniería y más. Paso a Paso: Cómo Aplicar la Integración por Partes Fórmula Integración por partes   Paso 1: Elección Estratégica de “u” y “dv” La elección adecuada de las funciones “u” y “dv” es un primer paso crucial. Generalmente, seleccionamos “u” de tal manera que su derivada “du” sea más simple que “u” en sí mismo, y elegimos “dv” de modo que su integral “v” sea más simple q...
Leer más
Imagen
Método  de discos y arandelas    en esta clase compre di un poco las dos fórmulas que se utilizaron en esta clase, pero a la hora de los ejercicios se me dificulto cuando me presentan la función y la tengo que pasar con respecto a x si está en y creo que con la practica puedo mejorar Podemos tener una función, como esta: Y hacerla girar alrededor del eje x, así: Para encontrar su  volumen  podemos  sumar una serie de rebanadas en forma de discos : La cara de cada disco es un círculo: El  área de un círculo  es  π  por radio al cuadrado: A =  π  r 2 Y el radio  r  es el valor de la función en ese punto   f(x) , por lo tanto: A =  π  f(x) 2 Y el  volumen  se encuentra sumando todos esos discos usando  integración : Volumen =  b a   π  f(x) 2  dx Y esa es nuestra fórmula para  sólidos de revolución mediante discos En otras palabras, para encontrar el volumen de revol...
Leer más