CONTINUIDAD DE UNA FUNCION
aprendizaje: aprendí a como realizar una continuidad de una función de manera fácil como nos lo explicaron en la clase
que el punto x= a tenga una imagen
que existe el límite de una función en un punto x= a
que la imagen y el punto coincidan con el límite de la función en el punto
de esa manera podrás saber si tu función es continua o descontinua
Verifica si la función:
es continua en el punto ![]() .
.
Primero calcularemos el límite:
Observa que la función está definida de una manera por la izquierda y de otra por la derecha de ese punto. Así que tendremos que calcular los dos límites laterales y verificar que coinciden. Empezamos calculando el límite por la izquierda:
Ahora calcularemos el límite por la derecha:
Como los dos límites laterales son iguales, el límite ![]() existe. Ahora verificamos que la función está definida para
existe. Ahora verificamos que la función está definida para ![]() . Observa que en la definición, la expresión
. Observa que en la definición, la expresión ![]() nos indica que debemos usar la primera rama de la función:
nos indica que debemos usar la primera rama de la función:
Además, podemos ver que ![]() , por lo que la función sí es continua en
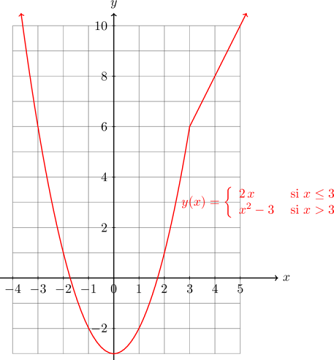
, por lo que la función sí es continua en ![]() . La gráfica de esta función se muestra a continuación:
. La gráfica de esta función se muestra a continuación:
Observa que la gráfica de la función es continua porque enel valor de las dos ramas coincide. Esto lo notamos del cálculo de los dos límites laterales. En general, puedes ver gráficamente si una función es discontinua si al graficarla ésta presenta un brinco, es decir, si no es posible dibujarla de un solo trazo. Las funciones escalonadas son discontinuas. Igualmente, las funciones racionales con denominador que se hace cero para al menos un valor de
.
Continuidad de una función - Aprende Matemáticas (aprendematematicas.org.mx)
continuidad de una función - Bing images




Comentarios
Publicar un comentario